4
Use of Signal Detection Theory as a Tool for Enhancing Performance and Evaluating Tradecraft in Intelligence Analysis
Gary H. McClelland
Many individuals and organizations make predictions of future events or detection and identification of current states. Examples include stock analysts, weather forecasters, physicians, and, of course, intelligence analysts. Consumers of these predictions need to know the expected accuracy of the forecasts and the confidence with which the predictions and putative detections are made. Those making the predictions need to know how well they are doing and if they are improving. Being able to assess prediction accuracy is especially important when evaluating new methods believed to improve forecast performance. However, in a problem that is not unique to the intelligence community (IC), forecasters are notoriously reluctant to keep scorecards of their performance, or at least to make those score-cards publicly available. As discussed extensively in Tetlock and Mellers (this volume, Chapter 11), Intelligence Community Directive Number 203 (Director of National Intelligence, 2007) emphasizes process accountability in evaluating IC performance rather than accuracy. This chapter suggests methods for improving the assessment of accuracy.
The chapter relies extensively on recent advances in assessing medical forecasts and detections, where signal detection theory specifically and evidence-based medicine more generally have led to many advances. Although medical judgment tasks are not perfectly analogous to IC analyses, there are enough strong similarities to make the examples useful. Just as physicians often have to make quick assessments based on limited and sometimes conflicting information sources with no two cases ever being quite the same, so too intelligence analysts evaluate and characterize evolving situations using partial information from sources varying in credibility.
In both medicine and intelligence analysis the stakes are often very high. That, combined with time pressure, can generate considerable stress for the person making the forecasts and detections. As the medical examples illustrate, rigorous evaluation of physician judgments and practices using the methods proposed in this chapter have improved medical outcomes substantially. It is reasonable to expect similar benefits if these methods are applied in intelligence analysis.
Without scorecards and assessment of accuracy of the many forecasts an individual or organization makes, judgments of forecaster performance are likely to be based on a few spectacular, newsworthy, atypical events. These events are more likely to be failed rather than successful predictions. For example, public assessments of the IC in this century are largely based on missing the 9/11 terrorist attacks and falsely claiming that Iraq had weapons of mass destruction (WMD). The dangers of forecasters being evaluated on the basis of a few events are obvious. The many day-to-day predictions that were correct are ignored, especially true negatives (e.g., no credit is given for not having invaded other countries that did not have these weapons). Also, post-hoc analyses of a few events are plagued by the problems of hindsight bias. Finally and perhaps most importantly, a few isolated events do not provide adequate data for assessing whether new methods (e.g., Intellipedia, A-Space, red cell analysis, having an overarching Office of the Director of National Intelligence) improve performance. Keeping score in the IC is likely to reveal much better day-to-day performance than they are given credit for by policy makers and the public.
Forecasters are not only reluctant to keep score, but also they often avoid making predictions with sufficient precision to allow scorekeeping. An important exception is contemporary weather forecasting that involves, for example, explicit probabilities of precipitation and confidence bands around predicted hurricane tracks. By contrast, many forecasts in other disciplines are too vague to support scorekeeping. In this context, an examination of unclassified National Intelligence Estimates (NIEs) from the past several years provides an interesting case study. Heuer (1999, pp. 152–153) explicitly warns: “Verbal expressions of uncertainty—such as ‘possible,’ ‘probable,’ ‘unlikely,’ ‘may,’ and ‘could’—are a form of subjective probability judgment, but they have long been recognized as sources of ambiguity and misunderstanding…. To express themselves clearly, analysts must learn to routinely communicate uncertainty using the language of numerical probability or odds ratios.” Sherman Kent (1964) had similar concerns and concludes:
Words and expressions like these are far too much a part of us and our habits of communication to be banned by fiat…. If use them we must in NIEs, let us try to use them sparingly and in places where they are least
likely to obscure the thrust of our key estimative passages…. Let us meet these key estimates head on. Let us isolate and seize upon exactly the thing that needs estimating. Let us endeavor to make clear to the reader that the passage in question is of critical importance—the gut estimate, as we call it among ourselves. Let us talk of it in terms of odds and chances, and when we have made our best judgment let us assign it a word or phrase that is chosen from one of the five rough categories of likelihood on the chart. [emphasis added]
However, in recent years, all NIEs contain a boilerplate page explaining that instead of using quantitative probability estimates that might imply overprecision, a set of probability words (“remote,” “unlikely,” “even chance,” “probably, likely,” and “almost certainly”) will be used instead. A graphic locates those words along an unnumbered probability scale. The actual use of such words in the predictions made in NIEs would allow some scorekeeping. However, a search of unclassified1 NIEs from the past several years reveal scant use of those words and much more frequent use of nebulous words like “could” that do not allow an assessment of accuracy. The boilerplate page includes this sentence: “In addition to using words within a judgment to convey degrees of likelihood, we also ascribe ‘high,’ ‘moderate,’ or ‘low’ confidence levels based on the scope and quality of information supporting our judgments.” Again, although associating such confidence words with predictions would facilitate scorekeeping, the issue is moot because the word “confidence” did not appear in a search of a number of recent NIEs.
This chapter suggests signal detection theory as a useful method for keeping score, develops some examples in the context of intelligence analysis, and describes some benefits of keeping score that have been achieved in other disciplines, such as weather forecasting and medicine.
SIGNAL DETECTION THEORY
Proposing signal detection theory as a method for keeping score—to evaluate prediction quality—in intelligence analysis, specifically, or detection and diagnosis, more generally, is neither novel nor surprising. The theory developed from the operations analysis (Kaplan, this volume, Chapter 2) of the military problem of using radar to detect aircraft. The seminal paper by Tanner and Swets (1954) was based on research funded by the U.S. Army Signal Corps. Lusted (1971) provides an early use of signal detection in
radiology, demonstrating its value for assessing radiologists, more informally trained assistants, and putative improvements in radiological examination systems. Numerous studies in radiology and medical diagnosis have relied on signal detection concepts. Several recent National Research Council reports on using polygraphs for lie detection (National Research Council, 2003) and evaluating emerging trends in cognitive neuroscience for identifying psychological states and intentions (National Research Council, 2008) both use signal detection concepts.
Basic Concepts of Signal Detection Theory
I briefly review the basic concepts underlying signal detection theory and illustrate them in the context of intelligence analysis. This is not meant to be a primer for signal detection concepts (see McNichol, 2004; Swets et al., 2000; Wickens, 2001), but instead an introduction and discussion of how signal detection measures could be used for scorekeeping within the IC. Whether or not one adopts signal detection for scorekeeping, knowledge of the concepts can usefully change how problems of detection and prediction are framed and discussed (see Oliver et al., 2008, for an example of the rhetorical power of signal detection in neurology). Sorkin and one set of colleagues (2001) and Sorkin and another set of colleagues (2004) provide excellent applications of signal detection of group or team decision making that may be especially relevant for IC applications (see Hastie, this volume, Chapter 8).
In essence, signal detection theory quantifies the ability of a detection system (whether it be an individual, a team of individuals, a test, a procedure, or a device) to distinguish between signal (i.e., an event of interest) and noise (i.e., background events of no interest). The most important aspect of this quantification is to separate the true accuracy of the detection system from the system’s (or individual’s) response bias—the propensity to be cautious and overwarn (false alarms) versus avoiding crying wolf, thereby underwarning (misses). These concepts and the important tradeoffs between them are discussed in detail below.
2 × 2 World View
Table 4-1 depicts signal detection theory’s rather simplistic 2 × 2 view of the world. The truth is whether there is a signal to be detected (e.g., dictator X will be overthrown next month, country Y has materials to make WMD, the image on the satellite photo is a mobile missile launcher) or there is noise (e.g., dictator X will continue, country Y does not have materials to make WMD, the image on the satellite photo is benign). Colloquially, a
TABLE 4-1 Signal Detection Theory’s 2 × 2 World View
|
|
Truth: |
||
|
Signal |
Noise |
||
|
Analyst Says: |
Alert |
Hit |
False alarm |
|
Quiet |
Miss |
Correctly quiet |
|
signal means “something is going on” that the intelligence analyst needs to alert someone about and noise means “nothing is going on.” The analyst can be correct by issuing an alert when there truly is a signal (a “hit”) or by correctly remaining quiet when there truly is no signal.
Note that the examples above appear to be of two different kinds: detection—the detection and identification of existing states of the world (e.g., country Y does have materials to make WMD)—and forecasting future states of the world (e.g., dictator X will be overthrown next month). Weather service tasks relevant to tornadoes illustrate both. A weather forecaster estimates the probability there will be tornadoes in a given time period, and weather observers try to detect tornadoes that have actually formed. So long as the validity of a forecast is eventually known, the distinction between detection and forecasting is not important for signal detection analysis, which unfortunately bears a name reflecting more its World War II origins in detection of airplanes than its wider current use.
Two types of errors The simplistic 2 × 2 world view of signal detection emphasizes that there are inherently two kinds of errors—misses and false alarms. Or there are errors of omission versus errors of commission. Absent a perfect detection system, the analyst must decide whether to err in the direction of a miss or a false alarm.
Graded response Although the analyst’s or decision maker’s response is dichotomous—alert or not—the strength of the evidence is likely to be a graded response on a more-or-less continuous scale. The inherent problem for the analyst is to decide when the graded evidence is strong enough to issue an alert.
Hit and false alarm rates Commonly used basic measures of detection performance are the hit rate—probability of correctly alerting when a signal is present—and the false alarm rate—incorrectly alerting when a signal is not present. Medical studies of signal detection often report the sensitivity
(equivalent to the hit rate, and referred to as the recall rate in some other fields) and specificity (equivalent to one false alarm rate). The more traditional hit rate and false alarm rate are used here, but it is important to recognize that similar measures with different names are sometimes used in different fields. They are all transformations of one another, so the choice is one of convenience.
Assessing detection performance The key issue in this context is how to use the hit and false alarm rates to assess the performance of the detection system, whether that system is an electronic device (e.g., the Preliminary Credibility Assessment Screening System, or PCASS), a human intelligence analyst, or the IC as a whole. If the system were simply guessing, we would expect the hit and false alarm rates to be equal, with the exact rate depending on the system’s propensity to “alert.” The performance equivalent to guessing is represented by the diagonal line in Figure 4-1, which depicts the relationship between the hit and false alarm rate. The system does better than guessing the extent to which the hit rate exceeds the false alarm rate.
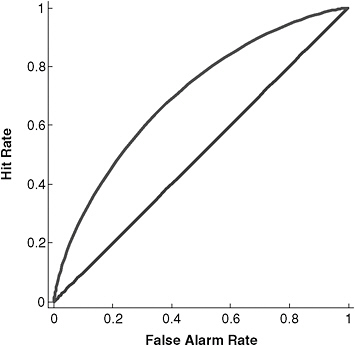
FIGURE 4-1 Inherent trade-off between hit rate and false alarm rate.
SOURCE: Generalized from Green and Swets (1966).
The performance of a moderately good detector is depicted in Figure 4-1 by the curved line above the diagonal.
The relationship between the hit and false alarm rates is constrained by curves similar to the one depicted in Figure 4-1, often referred to as ROC (for “receiver operating characteristic”) curves. The actual hit and false alarm rates, a point along the curve, is determined when the detector or analyst sets the threshold that the graded response must exceed before an alert is sounded. A conservative threshold—one requiring strong evidence—would produce relatively few false alarms, but consequently, also relatively few hits; this is represented by the open circle at the left lower end of the ROC curve in Figure 4-2. Such a conservative threshold would be appropriate when false alarms were feared much more than misses. If misses were to be avoided at all costs, a liberal threshold would be appropriate, such as the black circle at the upper right end of the ROC curve in Figure 4-2. Note, however, the high hit rate (equivalent to avoiding misses) comes at the expense of a high false alarm rate. The gray circle mid-way
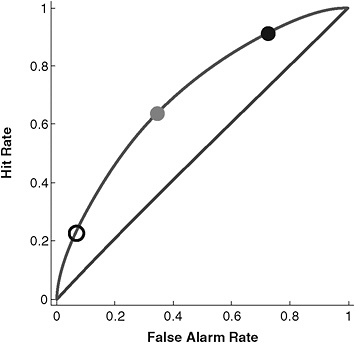
FIGURE 4-2 Differential weighting of misses and false alarms.
NOTE: Lower open circle represents fear of false alarms; upper black circle represents fear of misses; middle gray circle represents balance between the two fears.
SOURCE: Generalized from Green and Swets (1966).
along the ROC curve represents a balancing of the fears or costs of misses and false alarms. None of the marked points on the curve represent better or worse prediction, but simply reflect differential concern for the costs of misses and false alarms. Thus, it is not the actual hit and false alarm rates that characterize performance of the detection system. Instead, either the standardized difference between the hit and false alarm rates d′ = zHR– zFA R or the area under the ROC curve (AUC) represent detection accuracy. Figure 4-3 depicts ROC curves representing increasing discriminability as they are further from the diagonal line. An important feature of signal detection theory is that it separates the inherent capability of the detection system (represented by d′ or AUC) from the threshold motivated by relative costs of misses and false alarms. Hence, d′ or AUC should be used to assess the performance of detection systems, whether they be electronic devices or intelligence analysts.
Changing response bias The actual hit and false alarm rates are determined by the threshold used to change the graded response into an action.
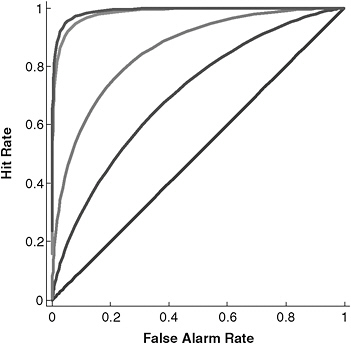
FIGURE 4-3 ROC curves representing increasing detection performance with increasing distance from the diagonal.
SOURCE: Generalized from Green and Swets (1966).
Numerous experiments have shown that human observers change their thresholds in response to change in the relative costs of misses and false alarms. It is not unreasonable to speculate that in the IC, a highly publicized mistake of one kind changes the threshold or response bias in a direction to reduce the likelihood of the kind of error made and thereby increase the likelihood of the other kind of error. An obvious example is that the miss of 9/11 was soon followed by the false alarm of Iraq WMD. There are other similar, but less dramatic, examples. For instance, on May 17, 1987 (during the Iran–Iraq War), an Iraqi fighter jet fired two Exocet antiship missiles into the USS Stark. Although the Iraqi airplane was observed and tracked, it was not deemed hostile and was sent a routine warning. The radar systems on the USS Stark failed to detect the two incoming missiles that killed 37 sailors and injured 21 others. This was a dramatic miss that likely changed the response bias of commanders of ships in the Persian Gulf to err on the side of false alarms rather than misses. Subsequently, on July 3, 1988, the USS Vincennes, a guided-missile cruiser with sophisticated detection systems aided by Airborne Warning and Control System (AWACS) flying in the area, mistook an Iranian commercial airliner taking off from a nearby airport for an Iranian fighter jet on the ground at the same airport. The USS Vincennes shot down the airliner, killing all 290 civilians aboard. This was a serious false alarm.
Strong experimental evidence in other contexts shows that changing the costs of misses and false alarms changes response bias and hence the rates for misses and false alarms (e.g., Healy and Kubovy, 1978). It would be surprising if the IC as a whole and individual analysts did not change their response bias as a consequence to well-publicized misses and false alarms. Importantly, different parts of the IC may be receiving different feedback and therefore be changing their response bias in directions that differ from each other. For example, terrorist analysts learned (and relearned, after the 2009 Christmas day bombing attempt on a transatlantic flight) that avoiding blame for “missing” something is much more important than raising many false alarms, creating a systematic bias to overstatement. This may be reinforced by the military origins of the IC with its penchant for “worst case” analysis because it is better to overestimate the capabilities of an adversary than to underestimate them. On the other hand, those in the IC charged with warning about general problems, such as warning about WMD capabilities, learned the opposite lesson from the Iraq NIE fiasco and may not lean far enough forward in making calls lest they be accused again of exaggerating the evidence or distorting it for political reasons and/or to avoid providing politicians with judgments that can easily be pushed beyond what analysts intended.
Effect of base rates Importantly, the above discussion omitted any consideration of a simple measure such as percentage correct as a measure of detection performance. This is because percentage correct is a function not only of the hit and false alarm rates, but also the base rate for occurrence of the signal. Base rate is the probability that the event of interest occurs in the population of events being examined. For example, when evaluating a medical screening test for, say, prostate cancer, the base rate—the proportion men screened who are expected to truly have prostate cancer—is critical for evaluating the performance of the screening test. Regardless of the detector’s inherent quality, extreme base rates can have a profound effect on the percentage of events classified correctly as signal or noise. Many authors provide their favorite examples of the nonintuitive consequences of ignoring base rates (e.g., Heuer, 1999, pp. 157–160, adapts an example to an intelligence problem; National Research Council, 2008, pp. 39–40), and many empirical studies have demonstrated that human decision makers often ignore the effects of base rates (e.g., Kahneman and Tversky, 1973; Bar-Hillel, 1980). Here is an example of a detection problem that illustrates the substantial effects of base rates on percentage accuracy even when the hit rate is very high and the false alarm rate is very low.
A company believes approximately 2 percent of its employees are drug users. The company administers a screening test to detect drug users. The test is very good with a hit rate of 95 percent and a false alarm rate of only 5 percent. Sara, selected at random for the screening test, receives a positive test result. What is the probability that Sara is actually a drug user?
Note that a drug test with such accuracy would represent extraordinary performance for a detector, represented by the most extreme (i.e., upper left corner) curve in Figure 4-3. For comparison, the detection performance of physicians diagnosing appendicitis or radiologists reading mammograms, for example, is not nearly as good. To answer the probability question for Sara, consider the expected frequencies in Table 4-2 of applying the screening test to 1,000 employees. With a base rate of only 2 percent, we would
TABLE 4-2 Expected Results for 1,000 People Screened by the Drug Test
|
|
Truth: |
|||
|
Drug |
Clean |
Total |
||
|
Drug Test: |
“User” |
19 |
49 |
68 |
|
“Clean” |
1 |
931 |
932 |
|
|
|
Total |
20 |
980 |
1,000 |
expect only 20 of the 1,000 to truly be drug users and the test would correctly identify 19 of those 20 (95 percent hit rate) as users. The remaining 980 employees are not drug users, but the test would incorrectly identify 49 of those 980 (5 percent false alarm rate) as drug users. The numbers in the table follow directly from the given base rate (2 percent), hit rate (95 percent), and false alarm rate (5 percent). Now consider the 68 employees who received positive drug test results. Of those 68, only 19 or 28 percent are truly drug users. Despite a highly accurate test, the probability that Sara (or anyone else with a positive test result) is truly a drug user is only 0.28. The low probability, despite a highly accurate test, is because the low base rate means the test is given many more opportunities (980 versus 20) to make a false alarm than to make a miss. The lesson is that even highly accurate detectors will produce many more false alarms than hits when detecting low base-rate events.
The important IC task of detecting hostile events toward the United States and its citizens is the task of detecting low base-rate events. Only a tiny fraction of all the passengers boarding airplanes or parking vehicles near Times Square are terrorists. Such detection systems will necessarily generate a large number of false alarms for each accurate detection of a terrorist. The signal detection model may be useful for communicating to IC customers and policy makers the inevitability of numerous false alarms in low base-rate detection situations.
Summary of Benefits of Signal Detection Theory
If one is going to keep score of prediction performance, signal detection theory provides an ideal framework. Its fundamental value is separating the effects of base rates, detector accuracy, and cut-point biases motivated by avoiding either false alarms or misses. In their abstract for a review chapter on clinical assessment, McFall and Treat (1999, p. 215) provide an excellent summary of the benefits of signal detection theory. One can read the following and substitute “intelligence assessment” for “clinical assessment.”
The aim of clinical assessment is to gather data that allow us to reduce uncertainty regarding the probabilities of events. This is a Bayesian view of assessment that is consistent with the well-known concept of incremental validity. Conventional approaches to evaluating the accuracy of assessment methods are confounded by the choice of cutting points, by the base rates of events, and by the assessment goal (e.g., nomothetic versus idiographic predictions). Clinical assessors need a common metric for quantifying the information value of assessment data, independent of the cutting points, base rates, or particular application. Signal detection theory (SDT) provides such a metric.
A rephrasing of the two last sentences appropriate for intelligence analysis might be:
“Intelligence assessors need a common metric for quantifying the information value of intelligence data and inputs, independent of the threshold biases used to change a graded response into action, the base rates of the hostile event to be detected, and whether the goal is to make a decision in a specific instance (e.g., does Country X have stockpile of biological weapons?) or a general rule (e.g., a policy that all airline passengers with certain characteristics be subjected to secondary screening). Signal detection theory (SDT) provides such a metric.”
An important benefit of using signal detection theory to evaluate and compare performance of individuals, teams, systems, procedures, and other factors is that it would require only a minimal, almost trivial, addition to the daily activities of the typical analyst. The only additional workload for the analyst would be to produce a probabilistic or categorical prediction of the future events being analyzed. Other researchers—not working analysts—could then subsequently assess the accuracy of those predictions in a signal detection analysis. That is, signal detection methods would not involve any immediate change in how the analysts did their work. Instead, SDT would be used by researchers to sift the wheat from the chaff among the methods and procedures analysts are already using or new ones that might be proposed.
BENEFITS OF KEEPING SCORE
A variety of measures might be used to score the performance of either individual analysts or more likely larger workgroups. A number of alternative, often mathematical, transformations of the traditional signal detection measures exist. For example, O’Brien (2002) uses similar measures—overall accuracy, recall, and precision—from the forecasting and text-retrieval literatures in an intelligence context to evaluate a pattern classification algorithm for predicting country instability. Studies in medicine often use closely related measures of sensitivity and specificity.
Regardless of whatever measures are used to keep score of prediction accuracy—even the less desirable percentage correct measure—studies in a number of contexts have shown that simply reporting scores as feedback have fostered improved performance without any other intervention. We all seem to be self-motivated to score better. An interesting example is an early study of probabilistic weather forecasting in the Netherlands (Murphy and Daan, 1984). In the first year, forecasters simply became acquainted with the process of making probabilistic forecasts. At the beginning of the second year, forecasters received feedback about their performance—they tended to overforecast. At the end of the second year, their accuracy had
markedly improved. Murphy and Daan (1984, p. 413) attribute the performance improvement “to the feedback provided to the forecasters at the beginning of the second year of the experiment and to the experience in probability forecasting gained by the forecasters during the first year of the program.” Although probabilistic forecasting and its improvement are almost surely more difficult in intelligence predictions than in weather predictions because of the quick and knowable feedback in weather forecasts, the IC might do well to study the history of probabilistic weather forecasts. Such forecasts were once rare (see Murphy’s 1998 review of the early history) and resisted, but now have become commonplace and expected with customers making important decisions based on probabilistic information.
Another context in which public scorecards have had substantial benefits is in the hospital setting, where nosocomial infections may occur. The Centers for Disease Control2 began the voluntary National Nosocomial Infections Surveillance (NNIS) system in 1970 with 20 hospitals. Now more than 300 hospitals participate (NNIS has recently been renamed National Healthcare Safety Network3). Hallmarks of the system are “standardized definitions, standardized surveillance component protocols, risk stratification for calculation of infection rates, and provided national benchmark infection rates for inter- and intra-hospital comparisons” (Jarvis, 2003, p. 44). Clearly the publication of infection rates has motivated hospitals to improve and increased searches for successful interventions, whose success in turn was monitored by changes in the published infection rates. In the 1990s, bloodstream infection rates declined 31–43 percent in intensive care units in hospitals participating in NNIS (Centers for Disease Control and Prevention, 2000). The rigorous definitions, careful monitoring, and especially the confidentiality of the NNIS system might provide a useful model for scorekeeping within the IC to improve performance.
EVIDENCED-BASED PRACTICE
Another obvious benefit of being able to keep score is the evaluation of innovations and even existing methods. Many methods used by or proposed to the IC have not been formally evaluated using randomized controlled trials. For example, intelligence analysis tradecraft not evaluated adequately include alternative competing hypotheses, PCASS, and even recent communication innovations such as Intellipedia and A-Space. The scientific literature is replete with examples of conventional wisdom, often based on observational data and anecdotes that turn out to be untrue when
|
2 |
Now the Centers for Disease Control and Prevention. |
|
3 |
For more information, see http://www.cdc.gov/nhsn/ [accessed October 2010]. |
scientifically evaluated. Medicine is full of examples of drugs and procedures that medical practitioners firmly believed to be effective, but turned out not to be when evaluated with randomized clinical trials.
An example of the mismatch between practitioner beliefs and actual facts is the conventional wisdom in many disciplines that treatment practice must be tailored to the idiosyncratic characteristics of individuals receiving treatment. However, when tested, the benefits of such tailoring are seldom supported. The education literature has countless articles about learning styles and the importance of tailoring educational material to those styles. However, critical evaluations and meta-analyses (e.g., Pashler et al., 2008) find little or no benefit for tailoring to learning styles. That is, the same good educational techniques are good for everyone, regardless of their putative learning styles. Similarly, treatments for alcoholics were believed to be most effective when tailored to specific patient characteristics. However, Project MATCH, a multisite clinical trial of alcohol treatment funded by the National Institute on Alcohol Abuse and Alcoholism to promote and test this hypothesis, eventually concluded that tailoring treatment to client attributes had little or no benefit (Project MATCH Research Group, 1997, 1998). These specific examples probably have no direct relevance to intelligence analysis except that they demonstrate that many strong beliefs of practitioners, developed over many years of experience, are often not confirmed by scientific experimentation.
The frequent mismatch between beliefs of practitioners and actual verified effects has motivated a vast literature on evidence-based practice. Entering the term “evidence-based” in a Google search in January 2010 generated approximately 48.1 million page hits in fields as diverse as medicine, education, and policing. However, so far only a few instances of evidence-based intelligence analysis have been found. Again, a detailed how-to for evidence-based practice is not appropriate for this chapter.4 Instead, I suggest by analogy how it might be useful in evaluating tradecraft practice in intelligence analysis. Evidence-based practice is not a panacea nor is it easy to implement, but the benefits of its application in other areas have been enormous.
A useful analogy might be the history of tonsillectomy (Grob, 2007) because it raises many issues similar to those faced in intelligence analysis. According to Grob, removing tonsils became popular once it became an easy surgery because it fit a contemporary disease model and because it stopped the recurrence of certain infections. However, there was no comparison of effectiveness relative either to a control group or to possible increases in other disease once the tonsils were removed. In fact, true randomized clinical trials would have been difficult or unethical because
|
4 |
Useful how-to information includes the website http://www.cebm.net [accessed October 2010] of the Centre for Evidence Based Medicine and Straus et al. (2005). |
true control groups would have required sham operations. Intelligence analysis may have similar problems implementing true randomized control trials. Only after innumerable tonsils had been removed were clinical trials begun in 1962. The hypothesis that the popularity of tonsillectomies might be motivated primarily by the pecuniary self-interests of the physicians is refuted by the fact that children of physicians had tonsillectomy rates as high or higher than those of other children (Bakwin, 1958). As tonsillectomies increased in frequency, they came to be expected and even demanded by the customers—parents of small children—and some argued for the prophylactic removal of tonsils in all children. Parents continued to request tonsillectomies even after enthusiasm waned among physicians. Only gradually have tonsillectomy rates declined, long after estimates of the benefits declined dramatically. The analogy of intelligence problems to the history of tonsillectomy is sobering. Evidence-based intelligence analysis is likely to be difficult and randomized trials may be nearly impossible (although simulated tournaments might be plausible substitutes). However, the history of tonsillectomy also suggests that evidence-based practice is possible with verified methods eventually supplanting conventional wisdom.
SUMMARY
Many fields akin to intelligence analysis, that is, those that make predictions and diagnoses in the face of uncertainty, have benefited from keeping score. Keeping score itself seems to motivate performance improvement without any specific interventions, presumably because units motivated to improve their scores relative to peers generate their own interventions. There is every reason to expect similar benefits of score-keeping for intelligence analysis. Scorekeeping is also necessary to be able to implement evidence-based practice to evaluate scientifically existing and proposed tradecraft for intelligence analysis. Although many possible measures might be used as scores, those of signal detection theory seem naturally suited to the uncertainty problems facing the IC that involve problems of low base rates, fluctuating biases toward false alarms and misses, and detector accuracy.
REFERENCES
Bakwin, H. 1958. The tonsil–adenoidectomy enigma. Journal of Pediatrics 52(3):339–361.
Bar-Hillel, M. 1980. The base-rate fallacy in probability judgments. Acta Psychologica 44:211–233.
Centers for Disease Control and Prevention. 2000. Hospital infection rates decline using CDC model program. Press release. Available: http://premierinc.com/safety/topics/patient_safety/downloads/10_nnispress300.pdf [accessed May 2010].
Director of National Intelligence. 2007. Intelligence community directive (ICD) 203: Analytic standards. June 21. Available: http://www.dni.gov/electronic_reading_room/ICD_203.pdf [accessed May 2010].
Green, D. M., and J. Swets. 1966. Signal detection theory and psychophysics. New York: John Wiley & Sons.
Grob, G. N. 2007. The rise and decline of tonsillectomy in twentieth-century America. Journal of the History of Medicine and Allied Sciences 62:383–421.
Healy, A. F., and M. Kubovy. 1978. The effects of payoffs and prior probabilities on indexes of performance and cutoff location in recognition memory. Memory and Cognition 6(5):544–553.
Heuer, R. J., Jr. 1999. Psychology of intelligence analysis. Washington, DC: Center for the Study of Intelligence, Central Intelligence Agency.
Jarvis, W. R. 2003. Benchmarking for prevention: The Centers for Disease Control and Prevention’s National Nosocomial Infections Surveillance (NNIS) system experience. Infection 31(Suppl. 2):44–48.
Kahneman, D., and A. Tversky. 1973. Psychology of prediction. Psychological Review 80(4): 237–251.
Kent, S. 1964. Words of estimative probability. Studies of Intelligence 8(4). Available: https://www.cia.gov/library/center-for-the-study-of-intelligence/kent-csi/vol8no4/html/v08i4a06p_0001.htm [accessed May 2010].
Lusted, L. B. 1971. Signal detectability and medical decision-making. Science 171(3977):1217–1219.
McFall, R. M., and T. A. Treat. 1999. Quantifying the information value of clinical assessments with signal detection theory. Annual Review of Psychology 50:215–241.
McNichol, D. A. 2004. A primer of signal detection theory. London, UK: Allen and Unwin.
Murphy, A. H. 1998. The early history of probability forecasts: Some extensions and clarifications. Weather and Forecasting 13(1):5–15.
Murphy, A. H., and H. Daan. 1984. Impacts of feedback and experience on the quality of subjective probability forecasts: Comparison of results from the first and second years of the Zierikzee experiment. Monthly Weather Review 112(3):413–423.
National Research Council. 2003. The polygraph and lie detection. Committee to Review the Scientific Evidence on the Polygraph. Division of Behavioral and Social Sciences and Education. Washington, DC: The National Academies Press.
National Research Council. 2008. Emerging cognitive neuroscience and related technologies. Committee on Military and Intelligence Methodology for Emergent Neurophysiological and Cognitive/Neural Research Methods in the Next Two Decades. Division of Behavioral and Social Sciences and Education. Washington, DC: The National Academies Press.
O’Brien, S. 2002. Anticipating the good, the bad, and the ugly: An early warning approach to conflict and instability analysis. The Journal of Conflict Resolution 46(6):791–811.
Oliver, R., O. Bjoertomt, R. Greenwood, and J. Rothwell. 2008. “Noisy patients”—Can signal detection theory help? Nature Clinical Practice Neurology 4(6):306–316.
Pashler, H., M. McDaniel, D. Rohrer, and R. Bjork. 2008. Learning styles: Concepts and evidence. Psychological Science in the Public Interest 9:106–119.
Project MATCH Research Group. 1997. Project MATCH secondary a priori hypotheses. Addiction 92:1671–1698.
Project MATCH Research Group. 1998. Matching alcoholism treatments to client heterogeneity: Project MATCH posttreatment drinking outcomes. Journal of Studies on Alcohol 59(6):631–639.
Sorkin, R., C. Hays, and R. West. 2001. Signal-detection analysis of group decision making. Psychological Review 108(1):183–203.
Sorkin, R., S. Luan, and J. Itzkowitz. 2004. Group decision and deliberation: A distributed detection process. In D. J. Koehler and N. Harvey, eds., Blackwell handbook of judgment and decision making (pp. 464–484). Malden, MA: Blackwell.
Straus, S. E., W. S. Richardson, P. Glasziou, and R. B. Haynes. 2005. Evidence-based medicine, 3rd ed. London, UK: Churchill Livingstone.
Swets, J. A., R. M. Dawes, and J. Monahan. 2000. Psychological science can improve diagnostic decisions. Psychological Science in the Public Interest 1:1–26.
Tanner, W. P., Jr., and J. A. Swets. 1954. A decision-making theory of visual detection. Psychological Review 61(6):401–409.
Wickens, T. 2001. Elementary signal detection theory. New York: Oxford University Press.


















